Spleenwort Fern




This is the spleenwort fern. It is a fractal generated by the IFS (Iterated Function System) method. In sum, the above shape is infinitely complex. No matter what resolution the actual shape is viewed at (this GIF representation, of course, does not possess infinite resolution), it will always appear infinitely fine. It can be printed or viewed at any resolution with no loss of quality.

And the cost of storage of this magnificent shape? All it takes to store this shape is four 2x2 transformation matrices, four 2x1 translational matrices, and four scalar probabilities. That, my friends, is a sum total of twenty-eight numeric values.



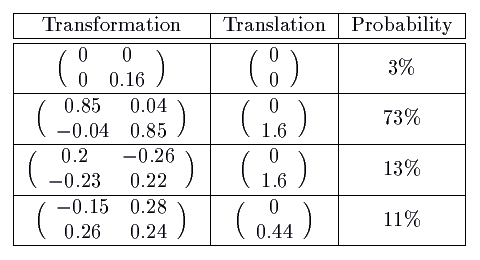
It is blindingly simple to construct the spleenwort fern above. Represent your coordinates as a vertical vector [[x][y]] and use the four sets of affine transformations above. For each iteration, select one of the transformation sets at random (given the weighted probabilities). Then multiply your current [[x][y]] by the transformation, add the translational vector, and plot the point. Iterate infinitely. And there you are, in living glory...

Under construction.
Much, much, more will be added as time passes.

Return to Chaos Hompage